소수를 구하는 알고리즘
소수란 약수가 1과 자신밖에 없는 수를 말합니다. 현재에 와서는 암호 분야에서의 사용으로 그 중요성이 부각되고 있습니다.
소수를 구하는 방법은 입력 범위까지의 정수 하나하나 2부터 그 정수전(n-1)까지 반복문을 이용하여 나눠서 하나라도 나누어 떨어지는 값이 있다면 제외 시키고, 나누어 떨어지는 값이 없다면 출력하는 방법을 사용했습니다.
소수를 구하는 알고리즘(N값 까지의 소수를 구함)
while ( i <= N ){
prime=true;
for(int n=2; n<i; n++){
if(i%n==0){ prime=false; }
}
if(prime==true){System.out.println(i); }
i++;
}
전체 소스코드
public class PrimeNumber {
int getNum;
PrimeNumber(int n){
this.getNum=n;
}
/**
* description : 소수를 구하는 메소드
*/
public void getPrime(){
int i=2;
boolean prime;
while(i<=getNum){
prime=true;
for(int n=2; n<i; n++){
if(i%n==0){
prime=false;
}else{ continue; }
}
if(prime==true){System.out.println(i); }
i++;
}
System.out.println("program is over!");
}
public static void main(String args[]){
PrimeNumber pn=new PrimeNumber(30000);
long start=System.currentTimeMillis();
pn.getPrime();
long finish=System.currentTimeMillis();
System.out.println(" 수행시간 : "+(finish-start));
}
}
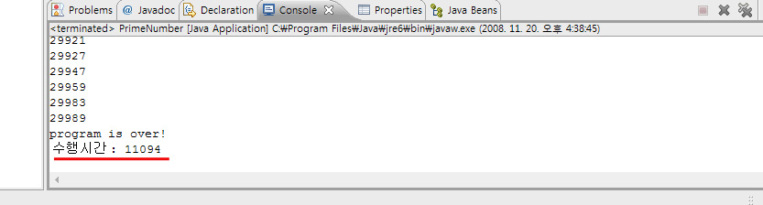
결과
위 코드는 소수를 찾기 위한 계산을 소수가 아닌 경우가 발생해도(즉, 나누어 떨어지는 경우가 생기는 경우) 반복문을 계속해서 수행합니다. 이 코드에 소수가 아닌 경우가 발생하면 반복문 수행을 중지 시키는 break; 를 걸면 소수를 구하는 시간이 훨씬 줄어듭니다.
수정된 코드
while(i<=getNum){
prime=true;
for(int n=2; n<i; n++){
if(i%n==0){
prime=false;
break; // 브레이크를 걸어줌
}else{ continue; }
}
if(prime==true){System.out.println(i); }
i++;
}
결과
위에 그림을 보시면 소스 가운데 추가한 break문 하나로 실행시간이 많이 줄었습니다. 단순한 예제이지만 시간 복잡도에 대한 예제로서 이 만큼 좋은 소스는 없는 것 같습니다.
더 시간을 줄이는 방법은 소수란 2,3,5,7,11를 제외한 2,3,5,7,11의 배수를 자연수에서 제외하는 방법을 취하고 남은 값으로 얻을 수 있습니다. 즉, 구하고자 하는 범위를 가진 배열을 0으로 초기화 시켜 위의 방식으로 소수가 아닌값을 1이나 다른 값으로 바꾸어 버리면 0을 가진 값만 소수로 남아 있습니다. 이 방법을 쓰면 수행시간이 600정도로 훨씬 짧아 집니다.
결국, 알고리즘이라는 것이 모든 경우의 수에서 시작하여 제외시킬 수 있는 부분을 제외하는 방식을 통해 최적의 알고리즘을 구현하는게 아닐까요??
'정보 처리 > 알고리즘' 카테고리의 다른 글
| 정렬 알고리즘 (0) | 2011.01.26 |
|---|---|
| N_Queen (Back Tracking 알고리즘) (0) | 2011.01.26 |
| 키값이 두개이고 값이 하나인 데이터를 정렬해야 한다면? (0) | 2011.01.26 |
| 최대 공약수(Greatest Common Divisor) 구하기 (0) | 2010.09.02 |
| 약수(Divisor) 구하기 (0) | 2010.08.28 |